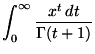mathematical
There exists a pair (r, x) such that r is a member of the set of all restaurants, and x is a member of the set of patrons. There exists a unique x such that, for some book b, the relation R(x, b) holds, where R(p, q) is true iff p is reading q. Let W be the set of all elements w where x is writing w. W is nonempty.
The cardinality of the set of players P such that iff q is a member of P, then q is playing Scrabble in some restaurant r (as posited above), is 2. The probability that a randomly chosen element from this set has a puzzled expression on his face is precisely one-half.
Without loss of generality, it can be shown that there exists a glass of water w such that the second derivative (with respect to time) of its distance to some floor f is -9.8 meters per second squared. It can be shown that for all such events, if the number of waiters near the point of impact prior to the event is k, the number of waiters near the point of impact after the event approaches 3k. There exists some positive number n such that there exists a patron p where p offers n napkins to each of the 3k waiters.
For some positive, even, integral number of hours fewer than four later, the unique element x mentioned above can be shown to belong to the set F where if y is a member of F then y is a geographically proximate friend of x. Furthermore, F possesses a bijection onto the set of conversations in which x is engaged.
There exists a set of cars C such that, for any three non-colinear elements of C the unique plane containing the three elements contains all the points in the path defined by some known bicyclist b. Although continuous, the path is otherwise fundamentally chaotic.